Integrating Spheres and Applications
Integrating sphere, as its name implies, is a spherical device with a reflective coating applied to its inside surface. A source of light is normally placed inside it and it will measure the total flux output of the source. It basically collects all the beams emanated from the object and reflected from the reflective coating of the inside of the sphere. It effectively integrates the measured light output from a source and hence the name integrating sphere.
An integrating sphere measures the total luminous flux from a light source and that has to be differentiated from illuminance. In photometry, the luminous flux is the measure of perceived power of light and is measured in units of lumen. On the other hand, illuminance is defined as the luminous flux per unit area and is measured in unit of lux (lumen/m2). The relation between luminous flux and illuminance in photometry, is the same as the relation between radiant power (measured in Watts) and irradiance (measured in Watts/m2) in radiometry. Figure below shows an integrating sphere diagram with a light source placed inside it.

Figure 1: A light source has been placed inside an integrating sphere. Total Luminous flux of the light source is measured.
There is another method of measuring the light output of a light source by an integrating sphere. An Integrating sphere usually has an entrance port and an exit port. One can place the light source right up against the entrance port such that all the emitted light is captured and the detector is placed at the exit port where all the reflected beams converge and hence the total flux from the light source can be measured this way. A baffle coated with the same coating as the inside surface, prevents the first reflected beam to enter the detector and makes sure that the beam makes a few bounces from the reflective coating before it enters the detector. Figure 2 shows a diagram of this configuration with the entrance and exit ports and the detector collecting all the reflected rays.
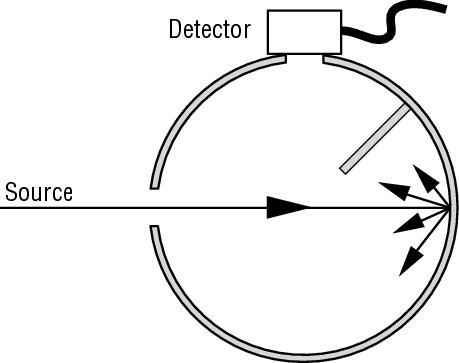
Figure 2: Configuration with the light source placed just outside the entrance port. A baffle
prevents the first reflected light to hit the detector
prevents the first reflected light to hit the detector
Another application of integrating sphere is its operation as a source of uniform radiance. If the detector is removed from the exit port, then the integrated light from the input source, which is quite diffuse, forms a uniform source which can be used to calibrate cameras, imagers, etc. Figure 3 shows this application.

Figure 3: Integrating sphere as a uniform light source used for camera calibration
In general, an integrating sphere can be used for optical, photometric, radiometric measurements. The spherical shape of the integrating sphere integrates the light inside of the sphere and makes it easier to capture light. The coating inside the surface of an integrating sphere is composed of different materials depending on the spectral range. Normally gold coating is used for IR range and Teflon is used for ultra-violet and visible range. If one wants to summarize all the different applications of the integrating sphere it can be done as follows:
General purpose light output measurement LED light output measurement Calibrations, for example for cameras and imagers where the integrating sphere is used as a uniform light source.Laser power measurements. Since the fraction of flux received by a photo-detector mounted at the sphere surface is nearly equal to the product of fractional surface area consumed by its active area multiplied by a constant of the integrating sphere (called sphere multiplier), it can be used to measure power of highly collimated , high power laser sources. Integrating sphere has been used to measure power from industrial CO2 lasers.Measurement of reflectance and transmittance of objects. An object can be mounted at the entrance port of the integrating sphere, where a source of light is behind it and the transmitted light through it is bounces off the reflective coating and is collected by the detector. The same measurement can be done by removing the object and directly measuring the output flux of the light source and hence calculate transmittance. Alternatively, the object can be mounted diagonally opposite to the entrance port and the reflectance of the object can be measured. Figure 5 shows the two configurations.
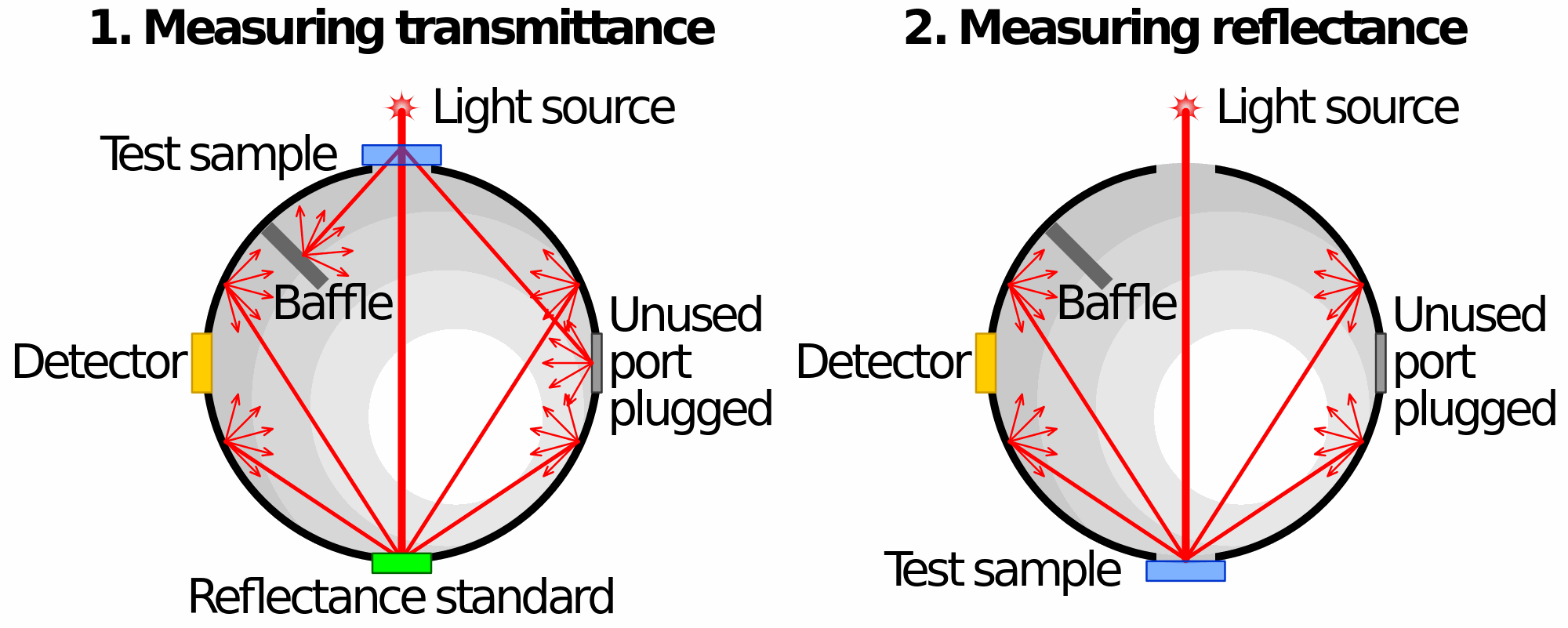
Figure 4: Transmittance and Reflectance measurements using an integrating sphere
To further understand the parameters which affect the performance of an integrating sphere, one has to introduce blackbody radiation concept first. The maximum energy that can be radiated by a body is called the black-body radiation. A blackbody is an object that is a perfect emitter and absorber of radiation and has an emissivity of 1. Max Planck in the early 1900’s formulated an equation which predicted the behaviour of a blackbody
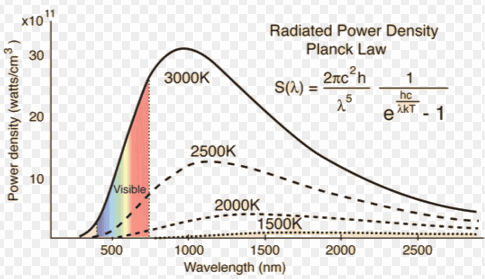
Figure 5: Radiated Power Density
One can see from the above graph, that peak of the black-body radiation shifts to shorter wavelengths as temperature rises. This is called the Wein’s displacement law and is expressed as . For example the sun which is a 5700 K blackbody, has its peak of radiation at 500 nm which is the maximum sensitivity of human eye (The eye has evolved to have maximum sensitivity to this wavelength) and the Earth which absorbs this radiation and re-emits in infrared (effectively a 300 K black-body emitter) has its maximum at 9.66 m. One can then define the “Emissivity” of an object as the ratio of the total radiation emitted by the object to that of a blackbody defined by the Planck’s formula. If an object emits less than a black-body, it has an emissivity of less than one and is called a “Gray-body”.
A material’s surface emissivity is a measure of the energy emitted when a surface is directly viewed. Surface emissivity is normally measured indirectly by assuming that e=1-reflectivity. A single energy bounce is measured and the reflected energy is measured. A mirrored surface may reflect 98% of the energy, while absorbing 2% of the energy. A good blackbody surface will reverse the ratio, absorbing 98% of the energy and reflecting only 2%. Effective emissivity is the ratio of the total amount of energy exiting a blackbody to that which is predicted by Planck’s law. Effective emissivity of a cavity type blackbody will normally be much higher than the surface emissivity due to multiple energy bounces inside the body cavity. Additional refinements to the term emissivity may be made by defining it in terms of the wavelength of interest, changes due to temperature effects etc. The simple concept of emissivity can very quickly become a very complex topic. Figure below shows a typical plot of surface emissivity.
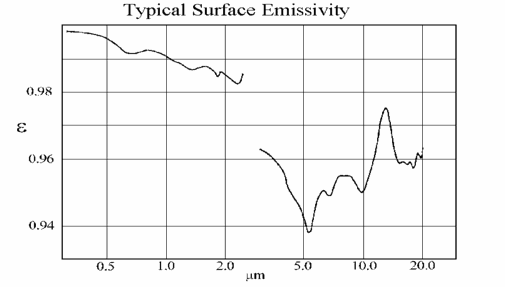
Figure 6: Typical Surface Emissivity